Seventh Open Letter to the Finance Committee: A Note on the Deduplication of Unique Identifiers
Sahana Sarkar on behalf of the Centre for Internet and Society (CIS) had sent in a Right to Information application on 30 June 2011 to Ashish Kumar, Central Public Information Officer, UIDAI. The UIDAI sent in its reply. Through the seventh open letter, Hans attempts to characterize in an abstract way the replies that CIS managed to elicit and makes some elementary observations.

With more than one signature, we have Y = 1 only when those of the applicant match the signatures in some other suite of such item by item; and Y = 0 then if at least one of his or her signatures fails to match any already recorded one.
Though the circumstance should be unlikely, a person who has already been registered may apply again to be registered: with fraudulent intent maybe: or simply because he or she has lost the document – some identity card, perhaps – which bears the identifier assigned to him or her by the UIDAI. And the possibilities here may be regarded as the values of a binary variable:
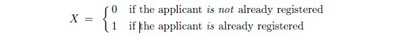
Though we are regarding X and Y as variables equally, and taking them for jointly distributed ones, there is an evident asymmetry between them. The exercise of trying to match a given suite of signatures to some set of other suites can be performed so long as the signatures remain available; but for a given applicant the values of X refer to events already past. Faced with an applicant of whom they may suppose no more than what he or she may disclose, the personnel of the UIDAI cannot directly estimate either of the two quantities:

We have p[X = 0] + p[X = 1] = 1 here, needless to say, so there is only one quantity that needs estimating. But it is worth emphasizing that even when an applicant declares himself to have been registered already— and has come, say, to have a lost card newly issued — the personnel of the UIDAI are obliged to remain agnostic about p[X = 1] : no matter how ready they are to believe him.[1]
That no individual should be assigned more than one identifier is an entirely evident desideratum: so the process of comparing the signatures of a fresh applicant to those already recorded must be a strict one. But the process of comparison should also make it very likely that, when a match of signatures does occur, the applicant is someone who has in fact been registered already. The chance that a genuinely new applicant’s signatures will match some already recorded suite should be very small: the proportion of such mistaken matches, among all matches, should be as low as possible. This proportion is usually denoted by p[X = 0 | Y = 1] : the conditional probability that X = 0 given that Y = 1 : the chance that, despite a match of signatures, the applicant has not in fact been registered already. The defining formula:
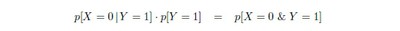
relates this conditional probability to the ‘absolute’ or ‘raw’ probabilities of the events [Y = 1] and [X = 0 and Y = 1] ; the second of which is sometimes said to be contained in the first.
Suppose that there have been N applicants thus far. It is usual to say N trials of X and Y have occurred; but only the outcomes for Y are known. Suppose that matches have been found some m times out of these N ; then N − m applicants will have been registered. With regard to these trials, set
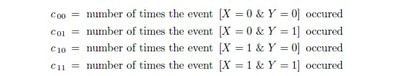
Note that these numbers are not individually known; but as the specified events exhaust the possibilities, we have c 00 +c 01 +c 10 +c 11 = N ; and we do know that
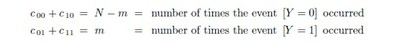
The ratio m/N would be a reasonable estimate of p[Y = 1] ; and (N − m)/N a reasonable estimate of p[Y = 0] = 1 − p[Y = 1] likewise. The quantity we are seeking is p[X = 0 | Y = 1] however: of which the ratio c 01/m would be a natural estimate. But unless we have some sense of the relative magnitudes of c 01 and c 11 the quantity
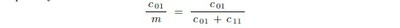
could be anything between 0 and 1 now. To estimate the relative magnitudes of c 01 and c 11 in any direct way would be difficult, because one has no purchase on how likely the events [X = 0 & Y = 1] or [X = 1 & Y = 1] are. So p[X = 0 | Y = 1] must be estimated directly, it would seem; and we shall come back to the question.
The reply we have received from the UIDAI indicates that 2.59 × 107 registrations — or successful ‘enrolments’, as they have put it — had been effected by 17.08.2011;while the ‘enrolments rejected’ came to 2.005 × 103 they say. Enrolments were rejected when ‘residents were duplicates’: if we take this to mean that an applicant was refused registry on account of his signatures matching some suite of signatures already recorded, then we may suppose that
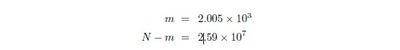
The False Positive Identification Rate, or FPIR, is defined in that reply as the ratio of the number of the number of false positive identification decisions to the total number of enrolment transactions by unenrolled individuals : if by “unenrolled individual” we understand an applicant of whom [X = 0] actually obtains, then in our notation we have
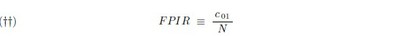
rather: which would be a natural estimate of p[X = 0 & Y = 1] now, and since
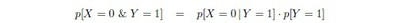
the ‘false postive identification rate’ thus construed could be bound, at least, if p[X = 0 | Y = 1] itself could be. At any rate, this latter proportion seems to be the most pertinent one here: p[X = 0 | Y = 1] is the conditional probability, of mistaken matches, that the UIDAI must strive to keep as low as possible.
The reply from the UIDAI defines a false negative identification as an incorrect decision of a biometric system that an applicant for a UID, making no attempt to avoid recognition, has not been previously enrolled in the system, when in fact they have. One is at a loss to understand how the personnel of the UIDAI are to determine when an applicant is making no attempt to avoid recognition. Putting that aside, the False Negative Identification Rate or FNIR would now appear to be p[X = 1 | Y = 0] : the probability that, despite his or her signatures not matching any already recorded suite, an applicant has in fact already been registered: and with our notation

now. But c 10 cannot be reliably estimated, again, because one has no purchase on how likely [X = 1 & Y = 0] is; and the conditional probability p[X = 1 | Y = 0] will have to be estimated or bound in some direct way as well.
The preceding paragraphs have asserted that, in order to estimate or effectively bound the identification rates being sought by the UIDAI, the conditional probabilities p[X = 0 | Y = 1] and p[X = 1 | Y = 0] will have to be addressed in some direct way: without any attempt to estimate the likelihoods of [X = 0 & Y = 1] and [X = 1 & Y = 0] by themselves, that is to say. There might be ways of reliably estimating these conditional probabilities; and the manufacturers of the devices that produce the signatures may have provided tight bounds on what they would be — when the devices are working properly, at least. But let us now consider how the UIDAI has elaborated on these rates.
Their reply to our second question states that the biometric service providers have to meet the following accuracy SLA’s for FPIR and FNIR:
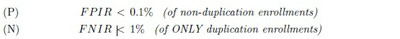
The condition of ‘non-duplication’ in the requirement (P) implies that the FPIR is being understood now as the formula in (†) above computes it: as an estimate of the conditional probability p[Y = 1 |X = 0]: since one already knows that [X = 0] for each enrolment here. Such an estimate could be made if one had obtained a sample of suites of signatures from distinct individuals — where no two suites in the sample could have come from the same individual — and compared each suite to every other: the proportion of matches found would be an estimate of p[Y = 1 |X = 0] now.[2]
The ‘biometric service providers’ the UIDAI has contracted with are presumably able to perform such experiments accurately. But an estimate of p[Y = 1 |X = 0] will not, as we shall momentarily see, by itself readily yield a usable bound on p[X = 0 | Y = 1] : on the crucial likelihood that, despite his or her suite of signatures matching a suite already recorded, an applicant has not in fact been registered.
The condition “ONLY duplicate enrolments” in the requirement (N) implies that the FNIR is being understood as an estimate of the conditional probability p[Y = 0 |X = 1] now: as one already knows that [X = 1] for each enrolment here. The biometric service providers should be able to estimate this probability as well. The FNIR as (‡) construes it is an estimate of p[X = 1 | Y = 0] rather; but a usable bound for this likelihood is readily got from p[Y = 0 |X = 1] now, for we may surely expect p[X = 1] < p[Y = 0].
Let us see if the requirement (P) will yield any usable upper bound on the crucial likelihood p[X = 0 | Y = 1]: which, to note it again, is what the UIDAI must seek to minimise. Consider the consequences when the FPIR is understood as (P) envisages. Taken together with formula (1) above we have
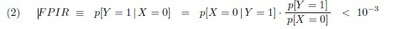
If we are not willing to wager on any upper limit appreciably less than 1 for p[X = 0] , we obtain
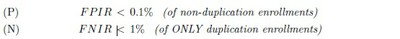
now.[3] Unless one can reasonably suppose that the event [Y = 1] never occurs, one must grant that p[Y = 1] > 0 . We have
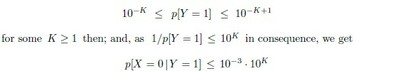
But this inequality yields a usable upper bound only when K < 3: only when K is 1 or 2 that is. In either case, only by supposing that p[Y = 1] > 10−2 will the accuracy mandated for the FPIR by the UIDAI yield a usable upper bound on p[X = 0 | Y = 1] . Since the UIDAI expects that p[Y = 1] < 10−2 surely, we must conclude now that the requirements it has imposed on its ‘biometric service providers’ will not help its personnel estimate an upper limit for the crucial likelihood that, despite his or her suite signatures matching some already recorded suite, an applicant for a UID has not in fact been registered already: which likelihood, to insist again, is what the UIDAI must seek to minimise.
The argument just made will seem perverse: but the calculation is perfectly general. Suppose an FPIR limit of 10−J is mandated; then, unless one is willing to wager an upper limit on p[X = 0] , one cannot get a usable upper bound on p[X = 0 | Y = 1] from this limit on the FPIR, used all by itself, unless one supposes that p[Y = 1] > 10−J+1.
To save writing, denote by L01 the crucial likelihood p[X = 0 | Y = 1] ; and suppose that is some desired upper bound on L01 now. Assume that the FPIR achieved by a service provider is an accurate estimate of p[Y = 1 |X = 0] ; then from (1) we get
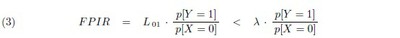
Now [X = 0] should not be a rare event at all, and, conversely, [Y = 1] should be a rare event.[4] So one should be able to set some reasonable upper limit to the ratio p[Y = 1]/ p[X = 0] : but without attempting any precise estimate, at all, of either individual probability. One may reasonably expect, for instance, that no more than one in a thousand applicants for a uid will already have been registered; and when p[X = 1] < 10−3 we will have
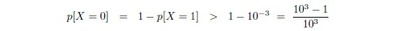
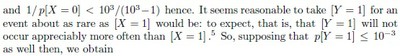
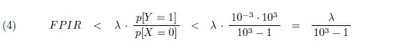
from (3) above. This calculation can be repeated with any number m in place of 3 here, of course, provided p[X = 1] < 10−m and p[Y = 1] < 10−m are both likely; and it seems entirely reasonable, now, for the UIDAI to insist that its biometric service providers meet the requirement.
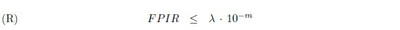
for some appropriate upper bound X on L01 . The considerations leading to (4) make it reasonable to insist on m _ 3 now; and recalling what L01 is — the crucial likelihood that, despite his or her signatures matching some already recorded suite of signatures, an applicant has not in fact been registered — the UIDAI will have to insist on some quite small bound X: for it would not want, too often, to refuse anyone a UID on account of a mistaken match of biometric signatures.[6]
It would be foolish to speculate on what the authorities regard as acceptable error here; but if the UIDAI is of a mind that such mistakes should happen less than one in a thousand times say, then, taking the minimal value of 3 for m in the suggested requirement (R), it should demand an FPIR less than 10−6 : a ‘false positive identification rate’ a thousand-fold less than the limit currently imposed.
[4]The event [Y = 1] must be just as rare, one supposes, as [X = 0] is frequent.
See the RTI application of 30/06/2011 [PDF, 15 kb].
Download the Seventh Open Letter here

